3.1 One-to-one Functions
A function f with domain A is called one-to-one if no two elements of A have the same image; that is
![]() implies that
implies that
![]() . This property implies that a horizontal line can intersect a one-to-one function at most once.
. This property implies that a horizontal line can intersect a one-to-one function at most once.
Examples
Example 3.1.1
Use the horizontal line test to show that the function
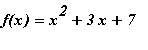 is not one-to-one.
is not one-to-one.
Of course we make a sketch.
| > | f:=x->x^2+3*x+7; |
![]()
| > | plot(f(x), x=-4..3); |
![[Maple Plot]](images/Lesson_035.gif)
Clearly there are many horizontal lines which intersect with this graph more than once.
![]() is an example as can be seen in the next graph.
is an example as can be seen in the next graph.
| > | plot({f(x), 9}, x=-4..3); |
![[Maple Plot]](images/Lesson_037.gif)
The function f is therefore not one-to-one.
Example 3.1.2
Use the definition of a one-to-one function to show that
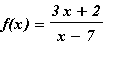 is one-to-one.
is one-to-one.
We will show that
![]() implies that
implies that
![]() .
.
| > | f:=x->(3*x+2)/(x-7); |
![]()
| > | eq:=f(x[1])=f(x[2]); |
![eq := (3*x[1]+2)/(x[1]-7) = (3*x[2]+2)/(x[2]-7)](images/Lesson_0312.gif)
| > | test:=solve(eq, {x[1]}); |
![]()
| > |
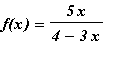 .
.
![[Maple Plot]](images/Lesson_0328.gif)
![[Maple Plot]](images/Lesson_0344.gif)
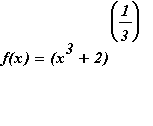 and its inverse.
and its inverse.
![[Maple Plot]](images/Lesson_0347.gif)
![[Maple Plot]](images/Lesson_0349.gif)