2.1
Examples
Example 2.1.1
Compute the Fourier cosine series for
![]() , on (
, on (
![]() ). Create a plot that shows the function
). Create a plot that shows the function
![]() and the partial sum of the first 20 terms of the Fourier cosine series on the interval
and the partial sum of the first 20 terms of the Fourier cosine series on the interval
![]() .
.
First code the orthonormal system, the inner product on (
![]() ), and the function
), and the function
![]() .
.
| > | phi[0]:=1/sqrt(Pi); phi[n]:=sqrt(2/Pi)*cos(n*x); dp:=(f,g)->int(f*g,x=0..Pi); f:=1+x; |
![]()
![phi[n] := 2^(1/2)/Pi^(1/2)*cos(n*x)](images/Lesson_028.gif)
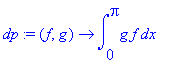
![]()
Create the Fourier constants, also called Fourier coefficients.
| > | c[0]:=dp(f, phi[0]); c[n]:=dp(f, phi[n]); |
![c[0] := 1/2*Pi^(3/2)+Pi^(1/2)](images/Lesson_0211.gif)
![c[n] := 2^(1/2)*(-1+(-1)^n)/Pi^(1/2)/n^2](images/Lesson_0212.gif)
| > | ps:=unapply(simplify(c[0]*phi[0])+'sum'(c[n]*phi[n], n=1..m), (m,x)); |
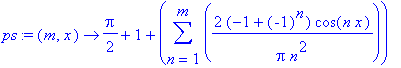
| > | p1:=plot(ps(20,x), x=-3*Pi..3*Pi): p2:=plot(f, x=0..Pi, color=green, thickness=4): display([p1, p2], scaling=constrained, view=[-3*Pi..3*Pi, 0..5]); |
![[Maple Plot]](images/Lesson_0214.gif)
| > |
Example 2.1.2
Compute the Fourier sine series for
![]() , on (
, on (
![]() ). Create a plot that shows the function
). Create a plot that shows the function
![]() and the partial sum of the first 50 terms of the Fourier sine series on the interval
and the partial sum of the first 50 terms of the Fourier sine series on the interval
![]() .
.
First code the orthonormal system, the inner product on (
![]() ), and the function
), and the function
![]() .
.
| > | phi[n]:=sqrt(2/Pi)*sin(n*x); dp:=(f,g)->int(f*g,x=0..Pi); f:=1+x; |
![phi[n] := 2^(1/2)/Pi^(1/2)*sin(n*x)](images/Lesson_0221.gif)
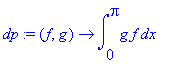
![]()
Create the Fourier coefficients.
| > | c[n]:=dp(f, phi[n]); |
![c[n] := -2^(1/2)*(-1+(-1)^n+(-1)^n*Pi)/n/Pi^(1/2)](images/Lesson_0224.gif)
| > | ps:=unapply('sum'(c[n]*phi[n], n=1..m), (m,x)); |
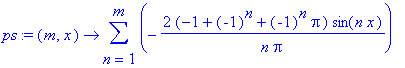
| > | p1:=plot(ps(50,x), x=-3*Pi..3*Pi): p2:=plot(f, x=0..Pi, color=green, thickness=4): display([p1, p2], scaling=constrained, view=[-3*Pi..3*Pi, -5..5]); |
![[Maple Plot]](images/Lesson_0226.gif)
| > |
Example 2.1.3
Let
![]() on (
on (
![]() ) and
) and
![]() , on [
, on [
![]() ) . Compute the Fourier series for
) . Compute the Fourier series for
![]() , and create a plot that shows the function
, and create a plot that shows the function
![]() and the partial sum of the first 50 terms of the Fourier series on the interval
and the partial sum of the first 50 terms of the Fourier series on the interval
![]() .
.
First code the orthonormal system, the inner product on (
![]() ), and the function
), and the function
![]() .
.
| > | phi[0]:=1/sqrt(2*Pi); phi[2*n]:=1/sqrt(Pi)*sin(n*x); phi[2*n-1]:=1/sqrt(Pi)*cos(n*x); dp:=(f,g)->int(f*g,x=-Pi..Pi); f:=piecewise(-Pi<x and x<0, 1, 0<=x and x<Pi, 1+x, undefined); |
![phi[0] := 1/2*2^(1/2)/Pi^(1/2)](images/Lesson_0236.gif)
![]()
![]()
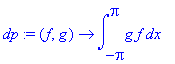
![f := PIECEWISE([1, -Pi-x < 0 and x < 0],[1+x, -x <= 0 and x-Pi < 0],[undefined, otherwise])](images/Lesson_0240.gif)
Create the Fourier coefficients.
| > | c[0]:=dp(f,phi[0]); c[2*n]:=dp(f, phi[2*n]); c[2*n-1]:=dp(f, phi[2*n-1]); |
![c[0] := 2^(1/2)*Pi^(1/2)+1/4*2^(1/2)*Pi^(3/2)](images/Lesson_0241.gif)
![c[2*n] := -Pi^(1/2)/n*(-1)^n](images/Lesson_0242.gif)
![c[2*n-1] := ((-1)^n-1)/Pi^(1/2)/n^2](images/Lesson_0243.gif)
| > | ps:=unapply(simplify(c[0]*phi[0])+'sum'(c[2*n]*phi[2*n]+c[2*n-1]*phi[2*n-1], n=1..m), (m,x)); |
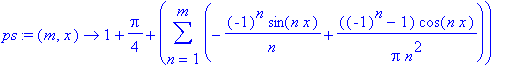
| > | p1:=plot(ps(50,x), x=-3*Pi..3*Pi): p2:=plot(f, x=-Pi..Pi, color=green, thickness=4): display([p1, p2], scaling=constrained, view=[-3*Pi..3*Pi, 0..5]); |
![[Maple Plot]](images/Lesson_0245.gif)
| > |
Example 2.1.4 (Problem 4, Section28, of the Textbook)
Find the Fourier series for
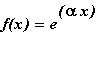 , on (
, on (
![]() ), where
), where
![]() . Use Euler's formula
. Use Euler's formula
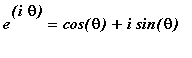 to write
to write
![a[n]+i*b[n] = 1/Pi*int(f(x)*exp(i*n*x),x = -Pi .. Pi)](images/Lesson_0250.gif) . Then, take
. Then, take
![]() and create a plot that shows the function
and create a plot that shows the function
![]() and the partial sum of the first 100 terms of the Fourier series on the interval
and the partial sum of the first 100 terms of the Fourier series on the interval
![]() .
.
Note that I used
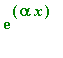 instead of the book's
instead of the book's
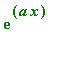 . This is necessary in order to avoid programming confusion between the
. This is necessary in order to avoid programming confusion between the
![]() in
in
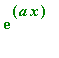 and the
and the
![]() in the coefficient
in the coefficient
![]() . Technically,
. Technically,
![]() is an element of the table
is an element of the table
![]() with alphanumeric index
with alphanumeric index
![]() .
.
First code the
orthogonal
system
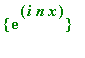 , the inner product on (
, the inner product on (
![]() ), and the function
), and the function
![]() .
.
| > | phi[0]:=1; phi[n]:=exp(I*n*x); dp:=(f,g)->int(f*g,x=-Pi..Pi); assume(alpha, real); f:=exp(alpha*x); |
![]()
![]()
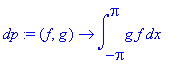
![]()
Create the Fourier coefficients. Note that, since the system
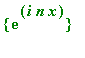 is not normalized, an appropriate multiplicative constant
is not normalized, an appropriate multiplicative constant
![]() needs to be introduced for the computation of the Fourier coefficients, much like the formulas for
needs to be introduced for the computation of the Fourier coefficients, much like the formulas for
![]() and
and
![]() we derived in the beginning of the course.
we derived in the beginning of the course.
| > | c[0]:=1/Pi*dp(f,phi[0]); c[n]:=1/Pi*dp(f, phi[n]); |
![c[0] := 1/Pi*(-1+exp(2*Pi*alpha))/alpha*exp(-Pi*alpha)](images/Lesson_0274.gif)
![c[n] := 1/Pi*(-1+exp(2*Pi*alpha))/(n*I+alpha)*(-1)^n*exp(-Pi*alpha)](images/Lesson_0275.gif)
Next, derive the formulas for
![]() and
and
![]() , where
, where
![]() is greater than or equal to
is greater than or equal to
![]() .
.
| > | a[0]:=combine(convert(c[0], trig), trig); a[n]:=combine(convert(Re(c[n]), trig), trig); b[n]:=combine(convert(Im(c[n]), trig), trig); |
![]()
![a[n] := 2*(-1)^n*alpha*sinh(Pi*alpha)/(Pi*alpha^2+Pi*n^2)](images/Lesson_0281.gif)
![b[n] := -2*(-1)^n*n*sinh(Pi*alpha)/(Pi*alpha^2+Pi*n^2)](images/Lesson_0282.gif)
| > | ps:=unapply(simplify(a[0]/2)+'sum'(map(factor, a[n]*cos(n*x)+b[n]*sin(n*x)), n=1..m), (m, x)); |
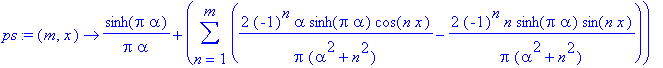
| > | p1:=plot(subs(alpha=1, ps(100, x)), x=-3*Pi..3*Pi): p2:=plot(subs(alpha=1, f), x=-Pi..Pi, color=green, thickness=4): display([p1, p2], view=[-3*Pi..3*Pi, -1..exp(Pi)]); |
![[Maple Plot]](images/Lesson_0284.gif)
| > |