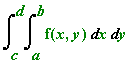Math 276

Calculus III

Fall 2001

Dr. Constant J. Goutziers

Department of Mathematical Sciences

goutzicj@oneonta.edu

Lesson 19

Double Integrals in Polar Coordinates

19.1 Double Integrals in Polar Coordinates

As explaned in class the double integral in Cartesian coordinates 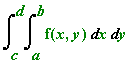can be translated into the following double integral in Polar coordinates: . provided that the region described by r = , , is the same as the region described by x = a..b, y = c.. d.

Examples

Example 21.1.1
Integrate the function 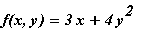over the region in the upper half plane bounded by 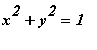and .

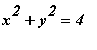First we enter the data and sketch the integration region. When working with Polar coordinates it is often helpful to incorporate the coordinate axes in the plot and have equal scaling on both axes.

> with(plots): with(student): with(oneonta):

Warning, the name changecoords has been redefined

> f:=(x, y)->3*x+4*y^2; bnd1:=x^2+y^2=1; bnd2:=x^2+y^2=4; bnd3:=y=0;

> implicitplot({seq(bnd||k, k=1..3)}, x=-3..3, y=-0.5..3, scaling=constrained);

Clearly we can integrate over r from 1 to 2 and over theta from 0 to .

> e1:=Doubleint(f(r*cos(theta), r*sin(theta))*r, r=1..2, theta=0..Pi);

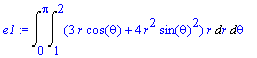
> e2:=Value(e1);

>

Example 19.1.1
Compute the volume of the solid above the cone 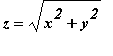and below the sphere .

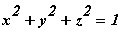First define the functions and plot the footprint of the solid. It should be clear that we need the top half of the sphere.

> f:=(x, y)->sqrt(x^2+y^2); g:=(x, y)->sqrt(1-x^2-y^2);

> bnd:=f(x, y)=g(x, y);

> bnd:=map(u->u^2, bnd);

> bnd:=map(u->u+x^2+y^2, bnd);

> bnd:=bnd/2;

> implicitplot(bnd, x=-1..1, y=-1..1, scaling=constrained);

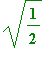From the plot and the equation of the boundary we derive that ranges between 0 and , andr ranges from 0 to . In order to simplify our coding, we will separately define the polar coordinates and substitute those into the cartesian equations of the cone and the sphere.

> polar:={x=r*cos(theta), y=r*sin(theta)};

> e1:=Doubleint(subs(polar, g(x, y)-f(x, y))*r, theta=0..2*Pi, r=0..sqrt(1/2));

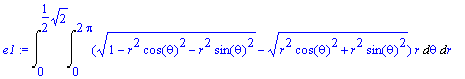
> e2:=simplify(e1, symbolic);

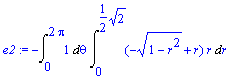
> e3:=simplify(Value(e2));

For the true graphics enthusiast it may be satisfying to sketch a 3D picture of this solid.

> p1:=plot3d(subs(polar, [x, y, f(x, y)]), theta=Pi/3..2*Pi+Pi/6, r=0..1, style=patch):

> p2:=plot3d(subs(polar, [x, y, g(x, y)]), theta=4*Pi/10..2*Pi+Pi/10, r=0..1, style=patch, color=red):

> p3:=plot3d(subs(polar, [x, y, 0]), theta=0..2*Pi, r=0..sqrt(1/2), color=[0.5, 0.5, 0.5], grid=[25, 5]):

> display([p1, p2, p3], axes=frame, scaling=constrained, orientation=[58, 64]);

The grey disk in the XOY plane represents the integration region.

>

Example 19.1.3
Compute the area enclosed by one leaf of the rose .

Now we know that the element of area dA = dx dy translates as dA = , we are able to express the area enclosed by a curve in Polar coordinates as a double rather than a single integral. The formula for the double integral may be easier to remember than the old single integral expression for the same area.

> f:=theta->cos(3*theta);

> polarplot(f(theta), theta=0..Pi, color=magenta, scaling=constrained, axes=boxed);

> area:=Doubleint(r, r=0..f(theta), theta=-Pi/6..Pi/6);

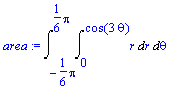
> answer:=Value(area);

>