Terry L. HELSER, Ph.D. 
Professor 
Chemistry Department 
S.U.N.Y. College at Oneonta,
Oneonta, N.Y. 13820-4015
Phone: (607)436-3518, or -3193; 
Fax: (607)436-2654
This appendix contains useful information on the metric system, pH and logarithms, and instructions on the care and use of pH meters and spectrophotometers. You can also go back to my home page or jump to the addresses at the bottom. 

THE METRIC SYSTEM

Linear Measure
1 mµ (10-6 mm) =
0.000000039 in
1000 mµ =
1 micron (10-3 mm) =
0.000039 inch
1000 µ =
1 millimeter =
0.039 inch
10 mm = 
1 centimeter = 
0.393 inch
10 cm = 
1 decimeter =
3.937 inches
10 dm = 
1 meter = 
39.37 inches
1000 m = 
1 kilometer = 1 km =
0.62137 miles
Weight Measure
1 microgram (10-6g) =
0.000000035274 ounce
1000 µg =
1 milligram (10-3g) =
0.000035274 ounce
1000 mg =
1 gram = 
0.035274 ounce
100 gms =
1 hectogram =
3.5274 ounces
1000 gms =
1 kilogram = 1 kg =
2.204 pounds
28.35 gms =
1 ounce
453.59 gms =
1 pound
907.18 kilograms =
1 ton
Liquid Measure
1 microliter (10-6L) =
0.0000338 fl. ounce
1000 µL =
1 milliliter (10-3L) =
0.0338 fl. ounce
1000 mL =
1 liter = 1.0567 quarts =
0.26418 gallons
0.47 liter =
1 pint 
0.95 liter =
1 quart
3.79 liters =
1 gallon 

Reference: L. J. Hale (1965) Biological Laboratory Data, "Methuen's Monographs," John Wiley & Sons, New York, 147 pp.
You can go back to the top, to the pH meter instructions or the closing from here. 


pH and Logarithms

Water ionizes slightly: H2O(H2O)n <--->H+(H2O)n + OH-. Direct measurements have determined that it is 0.00001% ionized at room temperature, so the concentration of each of the ions in pure water is 1 x 10-7 M. As you may have observed, the molar concentration of hydrogen ions (symbolized as [H+]) in water solutions is usually a very small number, indicated by negative powers of 10 (like 10-7 M = 1/10,000,000 M = 0.0000001 M). To avoid the use of such numbers, scientists defined a pH scale as the exponent of 10 that gives one over the molar concentration of hydrogen ions,

or: pH = log 1/ [H+] = - log [H+]. Thus, for pure water:
pH = log 1/10-7 = - log 10-7 = -(-7) = 7.
Since acids increase the [H+], the pH is less than 7. If the pH is greater than 7, a solution is basic.

1 <-- Acidic <--7 --> Basic --> 14 = pH scale. 


The following is a review of logarithms which should help you understand and use the pH scale. The logarithm of any number is the exponent ("power") of 10 (called a "base") that gives the number.

Thus: log 100 = 2, since 102 = 100, and
log 3.16 = 0.5, since 100.5 = 3.16.

The following relationships may help:
 
100 = 1
log 1 = 0
log (a x b) =
log a + log b
101 = 10
log 10 = 1
log a/b =
log a - log b
103 = 1000
log 1000 = 3
log 1/a =
- log a
10-1 = 0.1 = 1/10
log 0.1 = -1
log ab =
b(log a)
10-3 = 0.001 = 1/103 
log 0.001 = -3

  • In order to find the log of a number, convert it to scientific notation.
  • To find the number whose log is 6.8, separate the exponent into two, as follows:

    • 106.8 = 100.8 + 106, then look up 8000 in the body of the table to give N = 6,3,1, so 6.8 = log 6.31 + log 106 = log (6.3 x 106).
    Most calculators allow you to type "6.8", "2nd Function", "Log" or "6.8", "Inverse Log" to get the answer "6,300,000" or "6.3 e6", meaning 6.3 x 10 to the exponent 6.
  • To find the number ( [H+] ) whose log is -7.2 (as in, "The pH = 7.2, find the [H+]."), first realize that if 7.2 = pH = - log [H+], then [H+] = antilog or inverse log of -7.2 (multiply through by the minus).

    •  

     

    To solve this, add and subtract the next whole number exponent as follows:
    -7.2 + 8 - 8 = 0.8 + (-8), which = log (100.8 x 10-8 M). Look up 8000 in a table, which gives the Number 6,3,1. So, -7.2 = log 6.31 + log 10-8 = log (6.3 x 10-8 M). Thus, 6.3 x 10-8 M = [H+] that gives a pH of 7.2. 

    You can jump back to the top, to pH and Logarithms, to spectrophotometers or the closing here. 

    pH Meters

    Care and Use
    Before using a pH meter, the electrodes must be washed thoroughly with distilled water and blotted gently with tissue. The test and standard solutions should be the same temperature, since the pH of a buffer is temperature-dependent. For example, a common buffer has a pH of 7.0 ± 0.02 at 25°C, but at 0°C the pH is 7.12 ± 0.02. Other common errors in probe use are given below.
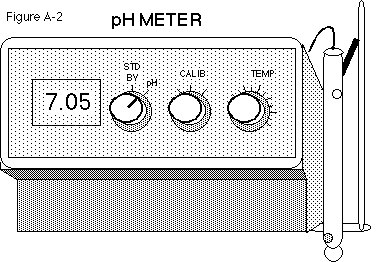
    To use the meter:
    1. Immerse the electrode(s) into the standard buffer solution and switch the left knob from stand by to pH (see Figure A-2).
    2. Adjust the meter with the calibration knob to the known pH of the buffer at that temperature.
    3. Rinse the electrode(s) and check the operation of the pH meter with another standard buffer, for example, a buffer of pH 4 or pH 10. Use the temperature knob to adjust, if necessary.
    4. Repeat steps 1-3 until the readings are stable.
    pH Meter ImageIdeally, the pH of each of the pair of buffers selected to calibrate the meter should bracket the expected pH of the test solution. If the pH of the second buffer is within 0.05 pH of the expected value, the pH meter is working properly.

    The use of two standard buffers of different pH is the only reliable way of checking a pH meter. Since the characteristics of the glass electrode change with time, the calibration of the meter must be checked at regular intervals.

    Once the meter is properly calibrated, the pH of the test solution may be determined. After use, rinse the electrode with distilled water. Since the glass tip of the electrode is very sensitive to dehydration, keep it immersed in distilled water when not in use. 

    You can go back to the top, to pH and Logarithms, or the closing from here. 

    Errors in pH Measurement

    The Sodium Error: Most pH-responsive glasses are somewhat sensitive to Na+. In fact, glass electrodes have been prepared which are more sensitive to alkaline earth cations than they are to H+ (the so-called cation electrodes). At high pH as little as 0.1 M Na+ can cause an apparent pH decrease of 0.4 unit. A curve for the correction of the sodium error is provided by the manufacturers of glass electrodes. This problem may be alleviated by the use of potassium salts rather than sodium salts, or by the use of the newer glass electrodes with reduced sensitivity to Na+.

    Temperature and Ionic Strength: The dissociation of acids and bases is temperature- dependent. Thus, the pH of a buffer solution can change dramatically with temperature. For example, tris(hydroxymethyl) aminomethane (Tris), a very commonly used buffer in biochemical research, has a dissociation constant which is strongly temperature-dependent.

    The activity coefficients of the charged species of a buffer are also affected by the ionic strength. Thus, addition of a salt at concentrations exceeding 0.025 M to a buffer solution can have profound effects on the pH. Further, dilution of a buffer will also generally have an effect on the pH. Thus, the pH of the final solution should be determined directly before it is used.

    Fouling of the Electrodes by Biological Samples: A pronounced drift in the pH of a solution may sometimes be noticed. In some cases, this drift may be caused by a small crack in the electrode; in other cases, however, it may be caused by the deposition of a thin coating of protein on the glass membrane. This coating may be removed by rinsing the electrode in a strong detergent solution.

    If the pH of samples containing suspended materials is determined, the fiber junction of the calomel electrode can readily become plugged. Since the fiber junction forms the salt bridge with the solution, it is imperative that it be clean. A plugged junction may be cleaned by briefly immersing the tip of the electrode in a solution of warm, concentrated nitric acid. 
    References:

    l. Bates, R.G., Determination of pH: Theory and Practice, Wiley, New York, 1964.
    2. Dole, M. The Glass Electrode, Wiley, New York, 1941.
    From: Wharton, D.C. and R.E. McCarty (1972) ExperimentsandMethods in Biochemistry, Macmillan Publishing Co., Inc., New York, N.Y. 
    You can go back to the top, to pH and Logarithms, the pH meter or the closing from here. 

    Spectrophotometer Use

    INTRODUCTION
    All compounds absorb specific types of electromagnetic radiation, with visible light being just one region of this spectrum. Some of the most important optical techniques in biochemistry depend upon this fact. For example, spectrophotometers that measure light absorption are used for quantitative work, since absorbance is proportional to the concentration of the absorbing solute. Thus, the course of a chemical reaction can readily be followed by using a color of light (wavelength) that is strongly absorbed by one of the products but not by any of the reactants. A simple instrument, the Spectronic 20, is described below.

    The Optical System
    The operation of this instrument is shown in the simplified diagram in Figure A-1.
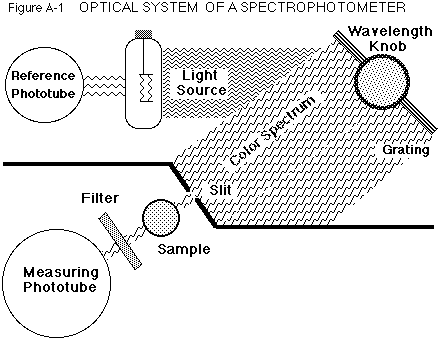    White light from the tungsten lamp is directed onto a reference phototube and a diffraction grating, which acts like a prism and spreads the light into a spectrum. Setting the wavelength sweeps the spectrum over the slit until only the selected color passes through and illuminates the sample in the chamber.

    Light which is not absorbed may pass through a filter (needed for the red region) before hitting the measuring phototube, where light is converted into an electrical signal. This is adjusted for variations in the lamp intensity by the reference signal, and then registered on the meter as absorbance and transmittance.

    Whenever the sample is removed from the chamber, an occluder automatically falls into the light path so that a zero light level may be set on the meter. A circuit operated with the right, front knob alters the lamp so zero absorbance can be set with a blank solution in the chamber.

    Operating Procedure

    1. Turn the power on. Turn the left knob on the front of the case clockwise until the meter needle is in the center of the scale.
    2. Allow to stabilize for at least 5 minutes before use.
    3. Select the wavelength. Turn the knob on the top, right of the case until the correct number is opposite the pointer visible in the window beside the knob.
    4. Zero the meter. Without a test tube in the chamber, adjust the left, front knob until the meter needle indicates infinite absorbance (= 0 transmittance). The sample chamber cover must be closed.
    5. Adjust for maximum absorbance. Fill a cuvette (test tube) with the blank solution (4 mL minimum), wipe the outside, align in the chamber, and close the cover. Adjust the right, front knob until the meter reads zero absorbance (= 100% transmittance).
    6. Measure sample absorbance. Fill the same cuvette, or one matched with the blank cuvette, with the sample solution. Wipe, align in the chamber, close the cover, and read the absorbance (or transmittance, if desired) from the meter.
    7. Guard against parallax errors by ensuring only one needle is visible in the mirror before taking the reading.
    Important:

    The meter must be adjusted for maximum absorbance (step 4.) each time the wavelength is changed. It is also necessary to occasionally check for meter drift from zero absorbance (step 3.). 
    That's all for now. Again, you can jump to the beginning, to my home page or the biochemistry or non-major's chemistry pages.

     

     

    If you have questions or comments, write the:

      Author of this page: Terry Helser - helsertl@oneonta.edu
      Web Coordinator: Steve Maniscalco - maniscsj@oneonta.edu
    Or return to the SUNY @ Oneonta Home Page to see where we live and work.
      Last Modified on 8/14/01

    Made on a MacMade with Mac OS